本文共 3611 字,大约阅读时间需要 12 分钟。
前情提要:
- 【递归】 这个难题中经常出现 return, return的作用只有两个: 1.返回指定类型的数据。 2.直接结束方法的调用。如下所示:
public void test8() { while (true) { System.out.println("ohh"); return;} - 深度优先搜索Depth First Search的思想——一条道走到黑,走到尽头再回退。
- 回退的实现就是用return。
运行结果为控制台输出 “ohh” ,如果没有return,while(true)永远成立,那么会无休止地输出"ohh",而实际上遇到"return",就会直接结束方法的调用,输出一遍"return"后,退出该方法。
以盒子/扑克牌数n=3为例。 假设有1-3号扑克牌和编号为1-3的三个盒子,现在需要把3张牌分别放到3个盒子中去,且每个盒子只能放一张牌,一共有多少种放法。 身临其境地去想,现在,我们走到第一个盒子前,我的手里有3张牌,放哪张牌呢?规定一个放牌规则:从小到大。因此,实现放牌需要一个循环,第box个盒子的放牌规则见以下方法:public void putInto(int box){ for(int i=1;i<=n;i++){ if(book[i]==0){ a[box]=i;book[i]=1; } }} 在以上代码中,book 数组用来判断手中是否有这张扑克牌,如果元素值为0,表示牌未放入盒子中,手里还有这张牌;如果值为1则说明牌已放入盒子,手里没有这张牌。a数组用来存放每个盒子里的扑克牌序号。
进入循环,则可按照从小到大的顺序,如果手里有这张牌,放入序号为box的盒子中,并把这张牌标记为1。 这时,第一个盒子里已放好扑克牌1。 接下来,我们需要去第二个盒子前,需要在方法中写入进入下一个盒子的语句:putInto(box+1);
用递归的思想,让方法自己调用自己。
在第二个盒子里放好扑克牌2。在第三个盒子里放好扑克牌3。这时,到了 putInto(box+1) 即putInto(4),说明这条道已经走到黑了,我们需要回退,在回退之前需要输出这种放牌方法。public void putInto(int box){ if(box==n+1){ for(int i=1;i<=n;i++){ System.out.print(a[i]);}System.out.println(); //每输出一种方法后换行return;//这里用return回退。}for(int i=1;i<=n;i++){ if(book[i]==0){ a[box]=i;book[i]=1; putInto(box+1);}}} 目前盒子一、二、三中放的扑克牌序号为1、2、3,并把该放置方法123输出(相当于第四个盒子),用return回退,这时我们站在了第三个盒子前,现在要做的事是将盒子三中的扑克牌收回到手中。回退后的操作需要写在putInto(box+1)后(因为回退"return"是直接结束方法,即结束putInto(box+1)的调用,从这个方法后继续执行语句):
book[i]=0;
这时,把第三个盒子中的牌3收回到手中。这时的i=3,i++,i<=n不成立,跳出循环,说明没有比原先牌3序号更大的牌可以放(因为需要按照从小到大的顺序,肯定就要从比原来序号大的扑克牌开始遍历,不然难道从当前序号开始???不对吧,那就没有改变牌的序号,比它小的开始???也不对,不符合从小到大的规则)。没有牌可以放了,我们就需要回退到上一个盒子,也就是盒子二,那么在for循环以外就需要一个return。
public void putInto(int box){ if(box==n+1){ for(int i=1;i<=n;i++){ System.out.print(a[i]);}System.out.println(); //每输出一种方法后换行return;//这里用return回退。}for(int i=1;i<=n;i++){ if(book[i]==0){ a[box]=i;book[i]=1; putInto(box+1);book[i]=0;}}return;} 那么,将会回退到 putInto(2) ,站在第二个盒子前,先把盒子二中的2号扑克牌收回到手中,这时的i=2,i++,i=3,i<=n成立,3号牌是在手中的,可以放入盒子二中。(总是从比原先放的牌号(如二盒中原来放的是牌2)大的牌开始,这是为了遵循从小到大的放牌规则)。放好牌后会去访问下一个盒子也就是盒子三。这不是回退到盒子三的,因此进入for循环,i是从1开始的,从小到大看哪个牌可以放入,则2号牌被放入盒子三。放好牌后会去访问下一个盒子也就是盒子四,即输出这个放牌方法132。
在输出后通过 return 回退到盒子三,先把盒子三中的2号扑克牌收回到手中,这时的i=2,i++,i=3,i<=n成立,可是3号牌不在手中,无牌可放。接下来,i++,i<=n不成立,退出循环。通过return回退到盒子二中,先把盒子二中的3号扑克牌收回到手中,这时的i=3,i++>n,跳出循环,通过return回退到盒子一中,先把盒子一中的1号扑克牌收回,这时的i=1,i++,i=2,i<3成立,2号牌是在手中的,把2号牌放入盒子一中。放好牌后去访问下一个盒子也就是盒子二,这时i从1开始,1号牌是在手中的,把1号牌放入盒子二中…方法是213。 输出后回退到盒子三,重复以上步骤…231…312…321 其实这和我手写排列组合的思路是一样的,第一个盒子先固定放1号牌,那么第二个盒子按照从小到大,就该放2号牌,盒子三自然而然也就放3号牌,或者第二个盒子放3号牌,盒子三放2号牌。第一个盒子放1号牌的也就这两种情况:123,132;接下来看第一个盒子放2号牌的情况:213,231… 这个程序中用到两处return,都是用来回退。第一种情况是走到第n+1个盒子,输出方法后,需要回退到第n个;第二种情况是在盒子前,收回该牌后,从比它大的牌开始遍历,遍历完牌发现没有可以放的牌时,需要回退上一个盒子继续去收牌。 如果在某个盒子放下了牌,就需要去下一个盒子,因此,完整的代码为:import java.util.Scanner;public class PlayCards{ private int[]book=new int[10];//用于标识该牌是否被放到盒子中,若被放下,值为1,没被放仍在手中,值为0 private int[]a=new int[10];//用于存放盒子对应的牌号码private int n=3; public void putInto(int box)//对应第box个盒子放扑克牌的规则 { if(box==n+1) //走到尽头,需要输出当前放置方案 { for(int i=1;i<=n;i++) { System.out.print(a[i]);} System.out.println();//每输出一组方案,需要换行一下 return;//return用于回退 } //按把手里的牌按从小到大顺序放入盒子中 for(int j=1;j<=n;j++) { if(book[j]==0) //该牌还在手里,可以放 { a[box] =j; book[j]=1;//改标识,说明该牌已被放入盒 //接下来需要去访问下一个盒子 putInto(box+1); //在访问下一个盒子后需要写的是回退以后的操作 //回退以后首先需要把当前盒子里的牌收回 book[j]=0;}} //遍历完牌发现没牌可放再回退,用return return; }} 在单元测试种写:
public class PlayCardsTest { PlayCards exam=new PlayCards(); @Test public void putInto() { exam.putInto(1); }} 运行结果为:
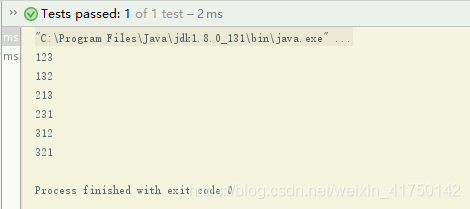
转载地址:http://sbjh.baihongyu.com/